Data visualization: The signal and the noise

Analyzing numerical data is an essential part of modern engineering practice. We explore trends, search for patterns, check relationships, and inspect distributions. Yet it can be rather challenging to consistently produce graphical representations of data that are legible, honest, and attractive. It is all too easy to confuse ourselves and mislead others.

Turning numbers into insights is no automatic process, and it still needs an analyst who will roll up his/her sleeves and become immersed in the data. To find that elusive signal amidst the noise, the human visual system is hard to beat. It just needs clean, clear, and honest visualizations to peer at, and producing those graphics requires deliberate, yet learnable, design decisions. The human visual system offers the highest bandwidth of any of our senses, and it is no coincidence that when we come to understand something, we say “I see.” We perform data analytics to gain insight.

This article is not a comprehensive graphic design style guide nor a software how-to manual. Rather, we wish to point out the differences between data and information and between opaque numbers and useful insights. Modern software can make data visualization almost too easy: with just a few clicks your dull numbers can dance to life as a colorful graph. That sort of convenience can suggest that there’s no need to stop and think about what you’re producing or to criticize the resulting graph. An effective engineer should be equipped with many questions to ask about any graphic they encounter or create. Has the appropriate type of plot been chosen? What might be obscured by the choice of axes? Is there other data that should be included within or alongside the figure?

Why graphs matter

Many data sets have striking or distinguishing features that remain hidden by their summary statistics. Consider the 13 distinct data sets represented as scatterplots in Fig. 1, which are taken from a recent paper by Justin Matejka and George Fitzmaurice. These data sets were craftily constructed to have matching means and standard deviations in both their vertical and horizontal ordinates as well as equal coefficients for their linear regressions. The scatterplots make clear how very different the relationships are with each data set. The plots in Fig. 1 make a strong case for Francis Anscomb’s injunction that “Graphs are essential to good statistical analysis.” There’s no need to summarize rich data sets with a few stingy numbers: pixels are cheap, so why not show as much of your data as possible?

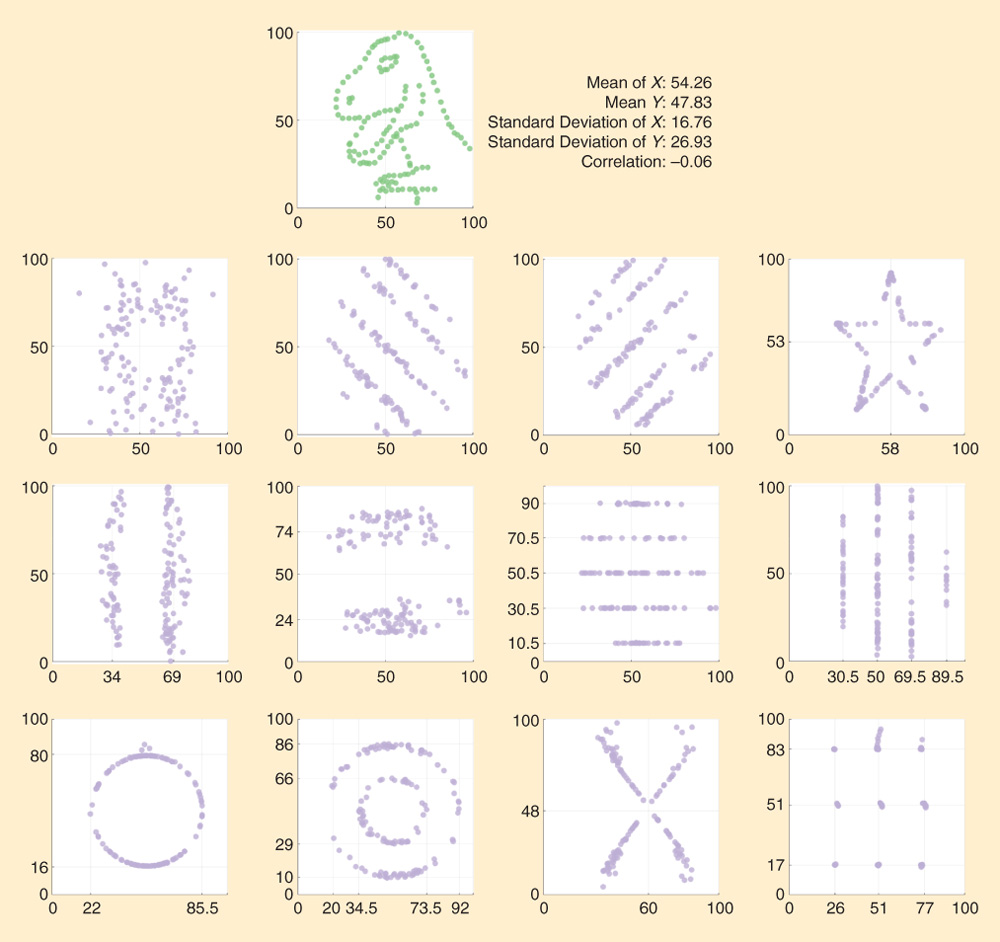
**Fig1** Scatterplots showing 13 distinct data sets that share certain summary statistics. The figure was redrawn using the publicly available numerical data from Matejka and Fitzmaurice (2017).

The eyeball test

The design of the ensemble of scatterplots in Fig. 1 is quite simple: they simply provide a unobstrusive window onto the underlying data. Like a fair referee or a well-made toupée, the mark of good design decisions is passing unnoticed. For instance, in this example, the axis ranges are the same for each data set, allowing them to be compared in a fair and even-handed way. By repeating the axes in a consistent fashion, a display of small multiples is achieved. Most software will automatically pick axis ranges based on each individual data set, so an equal treatment requires the designer to deliberately enforce consistency. The tick mark positions in Fig. 1 are also selected carefully to clearly label thresholds that are relevant to each particular data set. The ensemble seeks to emphasize the data itself, while de-emphasising other scaffolding as far as possible.

Another design decision imposed on each scatterplot pane in Fig. 1 is their absolute squareness. That is, not only are the axis ranges uniformly square [0 to 100], but each pane is also square in physical dimensions. Enforcing this ensures that the neatly circular feature to the bottom left can be identified by the eye as can the directly proportional 45° angle relationship shown in the middle of the first full row of panes.

Thinking more about graphical details

As the discussion of Fig. 1 has illustrated, the difference between an effective and unclear graph hinges on a sequence of design decisions. Here are some of the more common missteps found in engineering graphics:

Inappropriate, inconsistent, and poorly divided axes. Inappropriate suppression of axis zero points.
Fussy or unnecessary symbol markers and overly busy line dashings.
Graphs that are so reduced in size as to be unreadable when inserted into a single column of a two-column paper. Likewise, insufficient resolution and inappropriately small fonts.
Clumsy use of color coding, such as perceptually nonlinear mappings and graphs that do not reproduce in grayscale.
Counterintuitive plot aspect ratios and inconsistent scaling between comparable graphics.
A tendency to use needlessly elaborate graphics, such as three-dimensional bar charts in which the depth dimension has no meaning, or stacked bar charts rather than a line plot, or colored surface plots rather than heat maps.

The virtue of minimalism

The legendary English rockers Motörhead would ask for a live mix that had “everything louder than everything else.” This type of maximalist approach is not recommended when creating effective data visualizations. The graphic should reserve the greatest emphasis only for those elements that encode the underlying data, and it should downplay the prominence of other components as far as is practical.

It is easy to inadvertently create visualizations that contain lots of graphical clutter and scaffolding that distract the eye and deaden the figure’s impact. This hides the actual data and makes it hard to extract meaningful information and insights. Be suspicious of every supporting element in your graph. Every pixel or drop of ink given to lines, labels, or legends will pull the reader’s attention away from the interesting trends in the data itself.

So, how do you de-emphasize supporting elements to streamline your graph? The motto here is “remove to improve.” Systematically examine every single graphical element in your visualization and demand that each justifies its existence. Extraneous components should be summarily deleted, and those that can’t be purged outright should be toned down. Every graphical component must either 1) directly encode numerical variation or 2) provide the context that allows the proper interpretation of that data. To reduce the visual prominence of supporting elements, try making them thinner, less colorful, less central, and more translucent. Once you’ve tamed the clutter, you can amp up the prominence of your data-ink by making it brighter, bigger, and more attention-grabbing.

Consider the two graphs in Fig. 2. Note how much extra ink is used to produce Fig. 2(a). Various dubious design decisions include:

the ambiguous horizontal axis tick marks on Fig. 2(a)
unintuitive vertical axis range and divisions, labeled without a percentage symbol
a needlessly wordy vertical axis label (a % symbol would be more easily understood)
The heavy gray background of the plot area is visual deadweight
The grid lines feature very prominently (shorter tick marks would suffice)
no relationship between trace color and category is denoted
the legend box is distracting and visually heavy (adding a legend requires that the reader work, and you should never make your reader do extra work)
the data markers are too large (and they are not really needed at all).

Overall, the Fig. 2(a) display creates an impression that is dour, dense, and off-putting. It takes only moments to thin out certain components and smarten up the main points to create the more inviting display

in Fig. 2(b). Note, for instance, the directly labeled traces that avoid the need for a legend.

The importance of good axes

In a classic ballroom dance, the ladies wear bright, colorful dresses, while the gentlemen wear elegant, dark tuxedos, to provide a suitable frame to their partner’s glamour. The same principle holds for constructing the axes that frame a data visualization: all eyes on the numbers, please!

The axes are where the analyst must provide context, insight and structure to allow the data to be interpreted, but this should be done with deft minimalism, so that attention remains on the data itself. Default software-generated axes are too often a tell-tale sign of a careless visualization. There are many considerations that go into crafting useful axes, and each must be weighed carefully. For instance:

Axis ranges: Suppose that you’re creating a line graph showing the power flows into a power network that contains renewable generators. What is the most meaningful range for the axis? Left to its own devices, your software might find the maximum power export to be 95 MW, and it might use that as the axis maximum. Humans like round numbers, so there is always a better choice when possible: even if your data only varies between +95 MW and −75 MW, your axis should still run from
± 100 MW. If this leaves a lot of white space in the bottom half of your figure, that’s a feature not a bug. This negative space lets us infer, at a glance, that power flows are usually positive.
Axis tick marks: By default, software might carve up your axes into a half-dozen equal increments. So with our chosen axis range, the vertical axis ticks might march along as [−100, −60, −20, +20, +60, +100]. Are these the ideal intervals, though? For sure, zero deserves a place on every axis and certainly warrants a tick mark and corresponding grid line. Are 20 and 60 relevant thresholds? Can they be removed? Perhaps reactive power support only becomes available above +25 MW or curtailment becomes a possibility above +80 MW. All of these should be added and labeled accordingly. Remember: the axis exists to contextualize and frame your data, and only the analyst has the domain expertise to select the interesting thresholds.
Axis units: What choice of unit will allow your axes to give the most succinct context for the data? The internal format of your working data might be quite inappropriate. For instance, it is common to see time-series plots where the horizontal axis is labeled Minutes, and runs up into the thousands. This is unnatural: no one measures the time of day by specifying the number of minutes that have elapsed since midnight. Moving to hours would help but only marginally. If I see a big upramp in the output of a windfarm, my natural curiosity wants to know when this happened, in human terms. So, “shortly after lunch” is meaningful information, whereas “800 min after midnight” is an abstract and opaque factoid. For time-stamped data, the horizontal axis should be labeled in the 24-h clock format, such as “14:00.”
Axis shape: If you are interested in spotting temporal patterns in cyclical data, using circular axes might be the most appropriate, to keep 23:59 and 00:01 appropriately close! While these complex graphs require care to execute well, they are a useful tool for time-series analysis: consider the colorful example in Fig. 3.

**Fig2** Two views of the same synthetic data set, where (a) is bogged down with distracting clutter, whereas (b) is simpler, cleaner, and more attractive for a general audience.

**Fig3** Electricity generation over a 24-h period from hydroelectric dams in the northwest
United States. The shading indicates the age of the data presented. Different colors are used for different dams. Plot used with permission from (Huang, 2017).

Give the right message deliberately, not the wrong one accidentally

As we saw in Fig. 1, a data visualization can draw out details that are obscured by simple summary statistics. Unfortunately, just as a summary statistic can mislead, so can a badly thought-out plot. In his book How to Lie with Statistics, Darrell Huff provides many examples of plots that deceive the reader. These include line graphs that exaggerate trends by cutting off axes or altering the unit of measurement and bar charts that use area rather than height to exaggerate differences between categories. Another example is given in (Kirkham and Dumas, 2009), where the case is made that the improper use of a line graph, rather than a bar chart, helped to erroneously establish a spurious link between the measels, mumps, and rubella vaccine and autism. To avoid traps such as these, the author of any data visualization must check carefully that the data are being represented fairly. A careless choice of plot in a report can give a misleading impression or even lead research completely down the wrong track.

Too much and too little information

Consider the plots in Fig. 4. In Fig. 4(a), nine years of hourly wind capacity factors during winters in Great Britain have been plotted against the corresponding demand in that hour. From this plot, there does not seem to be any obvious relationship between instantaneous wind and demand level. In Fig 4(b), a cubic spline has been used to smooth the relationship between wind and demand. Considering this plot alone, there might seem to be a strong relationship between the two variables. The wind capacity factor at high demand seems to be around 0.15 lower than at low demand, which is a potentially worrying situation. Despite both plots in Fig. 4 being based on the same data, the reader could draw very different conclusions from each.

The problem here is that too much data has been included in Fig. 4(a). Any relationship between wind and demand has been obscured; perhaps the use of market transparency, or marginal distributions, could help to articulate the varying density of data here. Conversely, the plot in Fig 4(b) is misleading because it does not contain enough information. Given the huge spread in data seen in the plot in Fig. 4(a), a single smoothed line does not fully represent the relationship between the two variables. At a particular level of demand, the associated wind capacity factor has substantially more uncertainty than that implied by the use of a single deterministic line in Fig. 4(b). As shown in the plot, any level of wind output is possible at any demand.

Relevance of the plot to the message

**Fig4** (a) A scatter plot of hourly wind capacity factors against the prevailing hourly demand.
(b) A smoothed curve of the same hourly wind capacity factors against hourly demand.
Both plots use data from nine winter seasons in Great Britain. Data from (Staffel and Pfenninger, 2016; Staffel and Pfenninger, 2017).

Even if a plot perfectly represents the data it can still be misleading if the data are not relevant to the question being asked. In (Huff, 1954), accident statistics for different types of transportation are discussed as an example of how data can be irrelevant and misleading. The number of deaths occurring on train tracks in one year is given as a worrying 4,712. However, it turns out that this number includes those hit by trains in their car. Only 132 of the 4,712 deaths were actually train passengers.

The plots in Fig. 4 could be used to discuss the risk of power generation shortfall at times of high demands (i.e., will the wind power be there when we need it?). The problem is that the majority of the data points in these plots are irrelevant to the calculation of reliability metrics: power shortfalls only occur in Great Britain at times of very high demand and very low wind levels. Including corresponding thresholds on the axes could help to guide the reader here. Limited data in the extremes of a range can make it difficult to extrapolate relationships seen in the bulk of the data. When producing plots like these, it is important to ensure that any data presented are relevant to the broader research questions.

Spurious correlations

Spurious correlation occurs when the correlation between two variables can be explained by a third variable. Problems arise if this correlation is mistaken for a causal relationship when no such relationship exists. Relationships between variables in a plot should be subject to a healthy dose of suspicion, with additional analysis or further scientific investigation used to confirm any conclusions drawn.

**Fig5** (a) A scatter plot of hourly Great Britain solar capacity factors against hourly demand. Data are from nine winter seasons. The
trend has been removed from the demand data so that different years are comparable. A smoothed curve is drawn using cubic soothing
spline. (b) The mean diurnal variation in Great Britain solar capacity factor over the winter season (solid line) with 5% and 95%
quantiles (shaded region). (c) The mean diurnal variation in Great Britain demand over the winter season (solid line) with 5% and 95%
quantiles (shaded region). Data are from (Staffel and Pfenninger, 2016; Staffel and Pfenninger, 2017).

In Fig. 5(a), nine years of hourly solar capacity factors in winter in Great Britain have been plotted against the corresponding demand in that hour. The plot clearly shows that the solar capacity factor seems to be minimal at both high and low demand levels, but it can be high for medium demand levels. This plot alone does not, however, give us the full story. In Fig. 5(b), the average solar capacity factor in each hour over the winter season (and the associated 5% and 95% quantiles) is shown. In Fig. 5(c), the average demand in each hour over the winter season (with 5% and 95% quantiles) is shown. By looking at Fig. 5(c), it is clear why the relationship between demand and solar in Fig. 5(a) looks as it does. At low demands (overnight) and at high demands (early evening), there is no solar generation. At medium-sized demands (during the day), the solar generation is highest. Using Fig. 5(a) alone, and without explanation, could be misleading—it is not that demand is dependent on solar but rather both solar and demand are dependent on time of day.

Conclusion

Though we speak and hear thousands of words of every day, it can still be challenging to write convincing dialog. Likewise, even though we may have plenty of experience working with data, presenting it in a tangible way without distortions and distractions can be tricky. The creation of any type of data visualization involves a sequence of deliberate design decisions. Chefs know that the way food is plated truly affects the way it tastes: we eat first with the eyes. Likewise, the insights and impressions we infer from a visualization crucially depend on the way it is designed and presented, and these skills should be embraced by all ambitious engineers.

Footer